Egyenletesen (2018)
Click here for the english version! 

- 1 egyenlet/hét
- max. 280 karakter/bejegyzés
- közérthető leírás
52: Tömeg-energia ekvivalencia
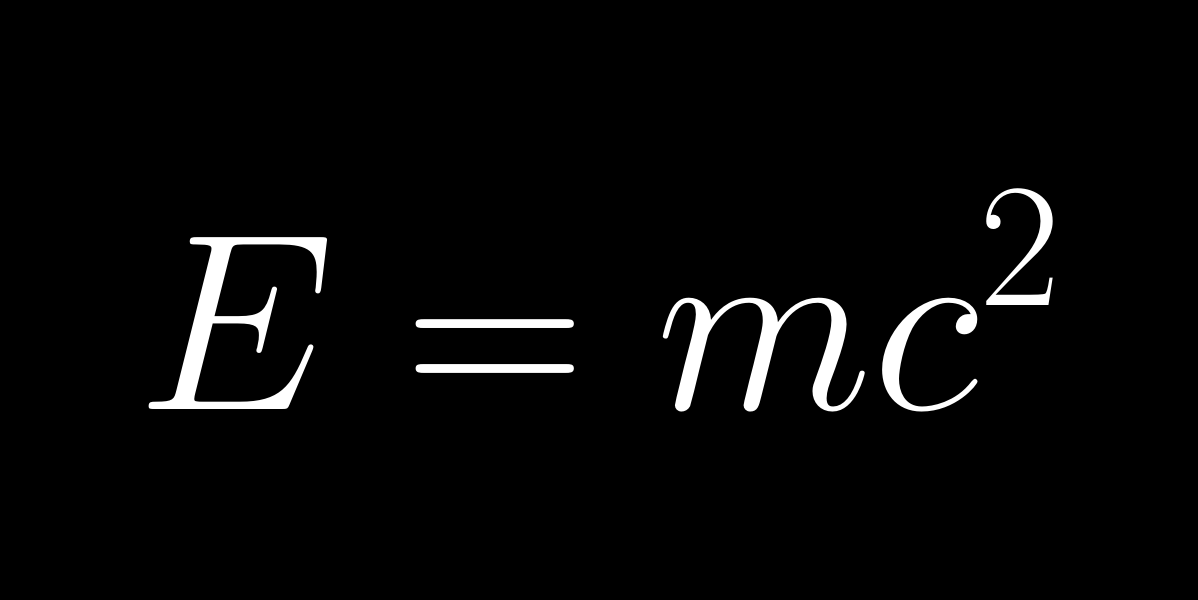
Einstein E=mc² képlete az energia és tömeg kapcsolatáról a világ leghíresebbje (c≈300000km/h a vákuumbeli fénysebesség). Ebben rejlik a kulcs az atomenergiához: a kötött és szétbomlott atommag pici Δm tömegkülönbsége hatalmas Δm×c² energia felszabadulását jelenti.
51: Yang-Baxter-egyenlet

Hogyan alakulnak ki a mágnesek? Miért fagy a víz jéggé? Ha jobban belegondolunk, ezek nagyon nehéz kérdések. A Yang-Baxter-egyenlet és az abból nyert R-mátrix segítségével mégis pontos válaszokat, megoldásokat tudunk adni ezekre.
50: Határozatlansági reláció
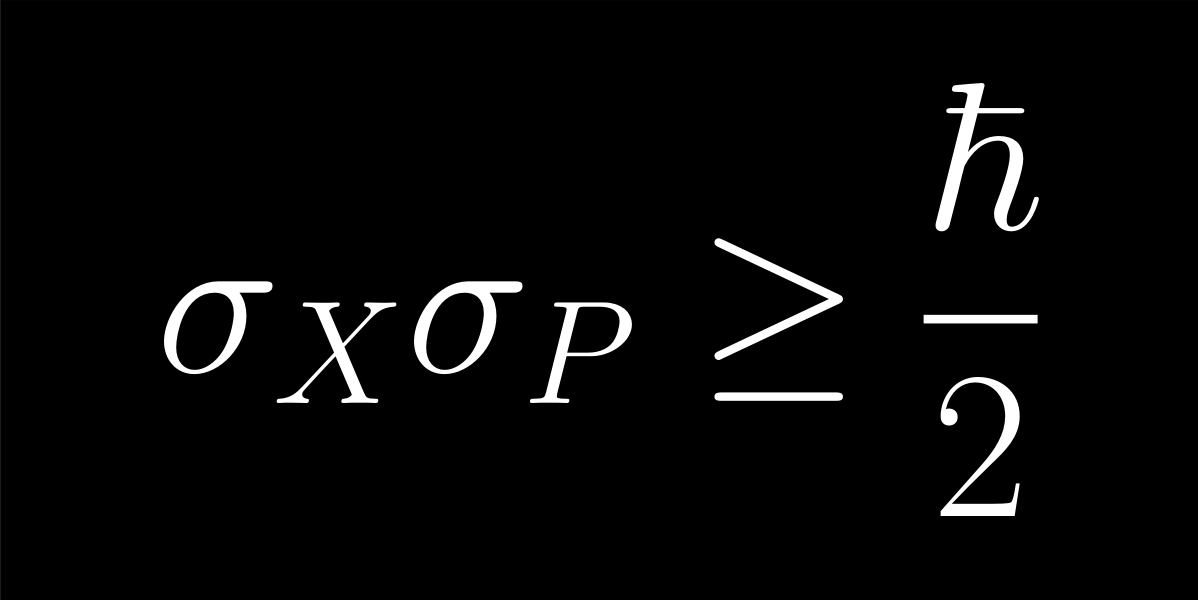
Egy hosszan búgó (szinuszos) alaphangot csak 1 jól meghatározott rezgésszám jellemez, de időben nehéz behatárolni. Egy rövid "fütty" jól lokalizált, de sok-sok felhang keveréke. A határozatlansági reláció a részecskék helyének és sebességének ugyanilyen kapcsolata.
49: Newton-Leibniz-tétel
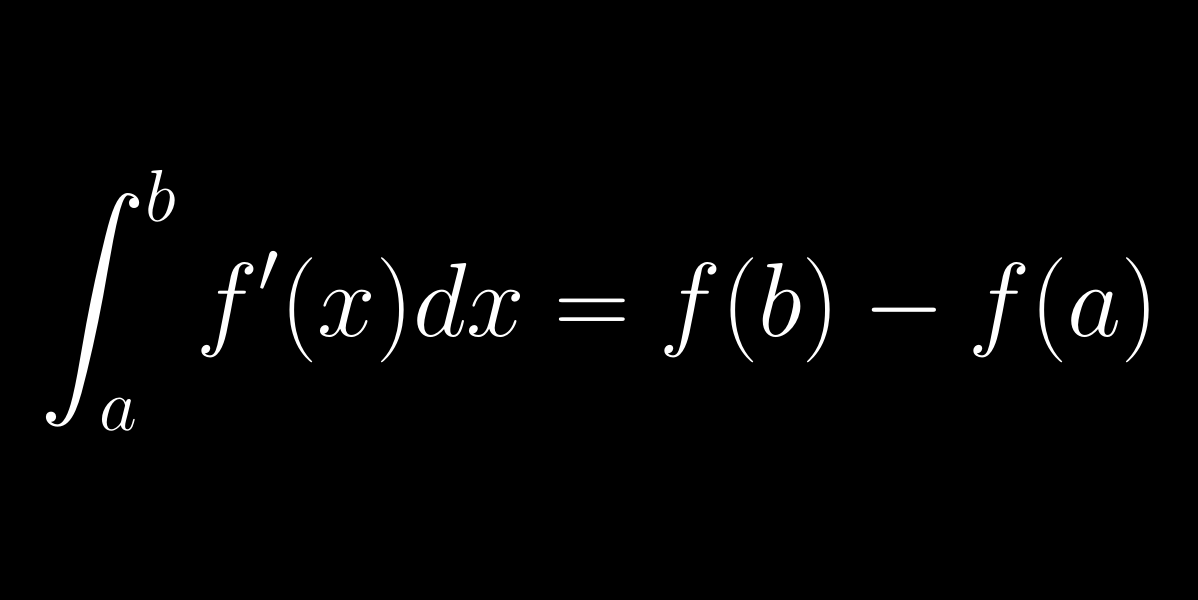
A fizikaórán megtanuljuk, hogy a megtett út = sebesség × eltelt idő (s=vt). De mi van akkor, ha a sebesség folyton változik? Meg tudjuk-e mondani mekkora utat autóztunk, ha csak a kocsi sebességét figyeljük? Igen, a Newton-Leibniz-tétellel.
48: Snellius-Descartes-törvény

A fény mindig a leggyorsabb úton terjed, de ez nem feltétlenül a legrövidebb út. Például vízben lassabb, mint levegőben, ezért gyorsabb, ha több időt tölt a levegőben. Emiatt van fénytörés a víz felszínén! A beesési szögeket és a sebességeket a Snellius-Descartes-törvény köti össze.
47: Minimax-elv

Minimalizálni a maximális veszteséget ugyanaz, mint maximalizálni a minimális nyereséget Ez a minimax-elv, a játékelmélet egyik alapvető eredménye, amit Neumann János bizonyított 1928-ban. Az elv a zéró összegű játékokhoz ad egy nyerő stratégiát.
46: Cramér-Rao-egyenlőtlenség

Szeretnénk a magyar emberek átlagos magasságát 1000 főből megbecsülni. Mit tegyünk? Vegyük az 1000 mérés átlagát? De mi garantálja, hogy nincs egy másik, ügyesebb számolás, ami jobban megközelíti a valódi értéket? Hát a Cramér-Rao-egyenlőtlenség.
45: sine-Gordon-egyenlet

A sine-Gordon-egyenlet egy gumiszál csavarodását írja le. Vannak stabil, lokalizált megoldásai, amiket szolitonoknak neveznek. Ezek hasonlóak a tömeggel és töltessél rendelkező részecskékhez. Emellett léteznek anti-szoliton és "szuszogó" megoldásai is.
44: Hamilton-féle mozgásegyenletek

Hamilton mozgásegyenletei Newton F=ma törvényének olyan újragondolása, ahol az erők helyett a teljes energia (H) játssza a főszerepet. Ez a megközelítés jelentette a kulcsot a statisztikus és kvantumfizika kidolgozásához a 20. század elején.
43: Háromszög-egyenlőtlenség

A háromszög-egyenlőtlenség nagyon egyszerű: egy séta A-ból B-be C-n keresztül (egyenes utakon) legalább olyan hosszú mintha egyenesen B-be mennénk. Mégis messzemenő következményei vannak; pl. az ikerparadoxon a speciális relativitáselméletben.
42: Felcserélési reláció

Ilyen felcserélési relációk alkotják a kvantummechanika alapját. Ez például a hely (X) és az impulzus (P) kapcsolatát fejezi ki: [X,P]=XP-PX=ih/2π, ahol h a híres Planck-állandó. Ebből következik a Heisenberg-féle határozatlansági-elv.
41: Binomiális tétel

"Ugyan ennek mi haszna az életben?" kérdezik gyakran a matematikusokat. Például, ha az (x+y)²=x²+2xy+y², (x+y)³=x³+3x²y+3xy²+y³ alakú (unalmas?) algebrai azonosságokat összefogó binomiális tételről van szó. Közben meg ezzel írható le a populációgenetika egyik alapvető törvénye!
40: Termodinamika második főtétele

A termodinamika második főtétele szerint egy zárt rendszer összentrópiája (rendezetlensége) sosem csökken. Bizonyos értelemben ennek köszönhető, hogy kepések vagyunk megkülönböztetni a múltat a jövőtől.
39: Cauchy-féle integrálformula
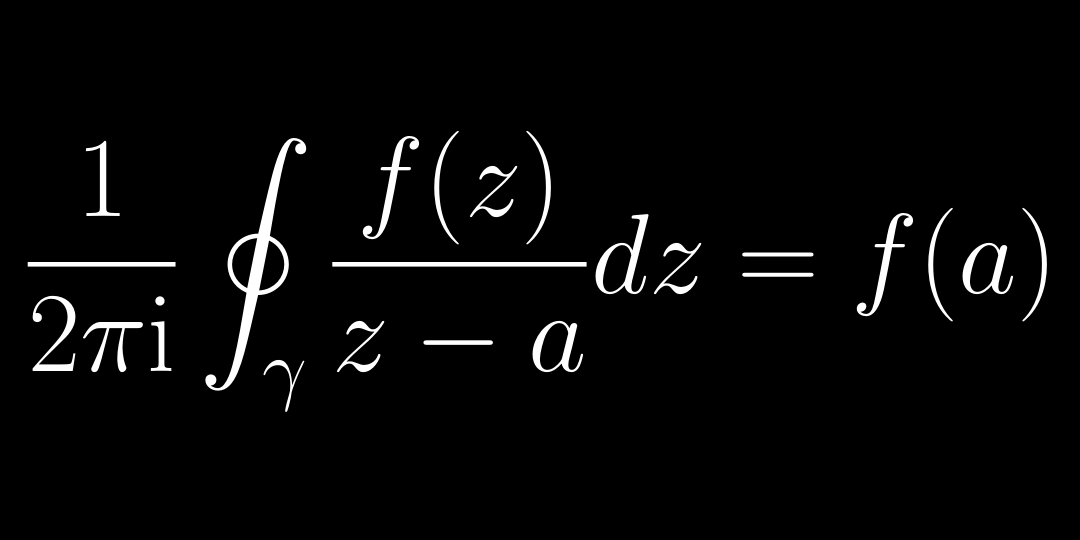
Egy felmelegített tányér peremét megtapogatva meg tudjuk-e mondani, hogy hány fokos a tányér közepe? Igen, csupán használnunk kell a Cauchy-féle integrálformulát, a komplex függvénytan egyik alapvető eszközét. Segítségével még az algebra alaptétele is bizonyítható!
38: Hullámegyenlet
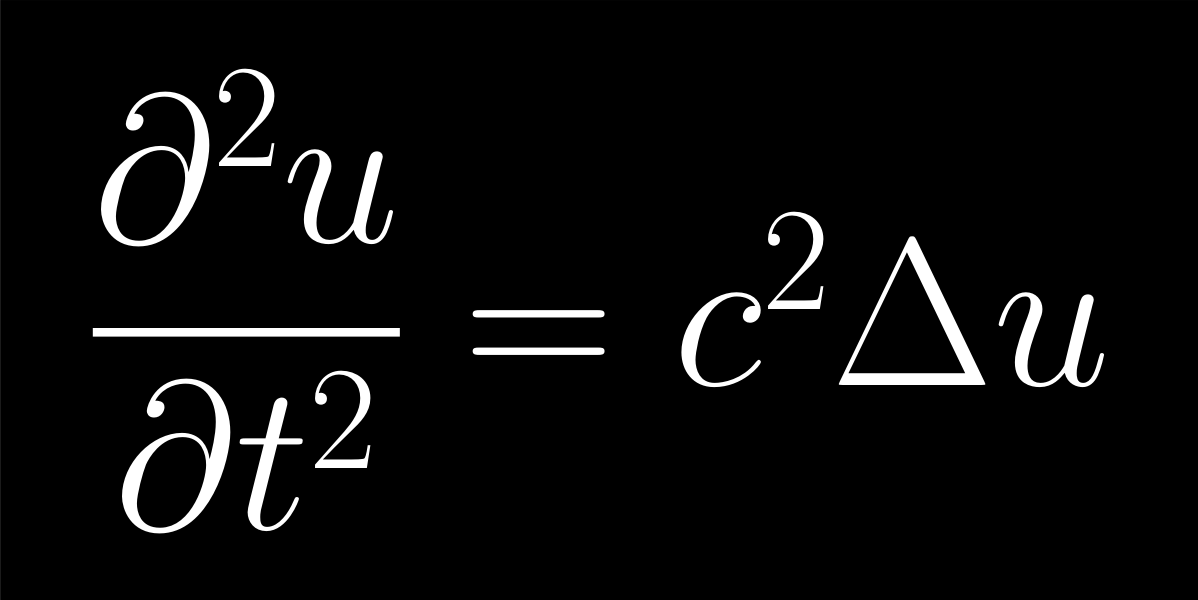
A megpendített gitárhúr, egy dob membránja, a WiFI jel, a fény és még megannyi "jel" terjedését/rezgését írja le ez az egyenlet, a hullámegyenlet, amiben a c paraméter a hullám terjedési sebessége.
37: Fibonacci-sorozat

Az állat- és növényvilágban sok helyen felbukkanó Fibonacci-számok a leghíresebb rekurzív sorozat tagjai. Minden szám az előző kettő összege, kezdve 0,1-gyel. Tehát a sorozat 0,1,1,2,3,5,8,13,... a szomszédok hányadosa pedig az aranymetszés ϕ≈1,618 arányszámához tart.
36: Euler-Lagrange-egyenlet

Milyen alakú egy függőágy? És egy kereten kifeszülő szappanréteg? Hogyan tisztítható meg egy zajos/szemcsés fotó? Ezekhez hasonló kérdéseket önt matematikai formába az Euler-Lagrange-egyenlet, ami egyben a részecskefizikusok alapeszköze.
35: Gauss-Bonnet-formula

Hogyan tudja egy hangya eldönteni, hogy labdán vagy úszógumin sétál? Úgy, hogy a felületet bejárva összegzi annak görbületét és alkalmazza a Gauss-Bonnet-formulát. A kapott szám 2π(2-2g), ahol g a lyukak száma. Ha az eredmény 4π, akkor labdán, ha 0, akkor úszógumin van.
34: P vs. NP

Egy Sudoku megoldása nagyon nehéz is lehet, de a megoldást mindig könnyű ellenőrizni. A megoldás NP, az ellenőrzés P bonyolultságú. Létezik-e P megoldási módszer? Ez a számítástudomány egyik legnagyobb megválaszolatlan kérdése. A megoldónak 1 millió dollár jár.
33: Időfüggetlen Schrödinger-egyenlet
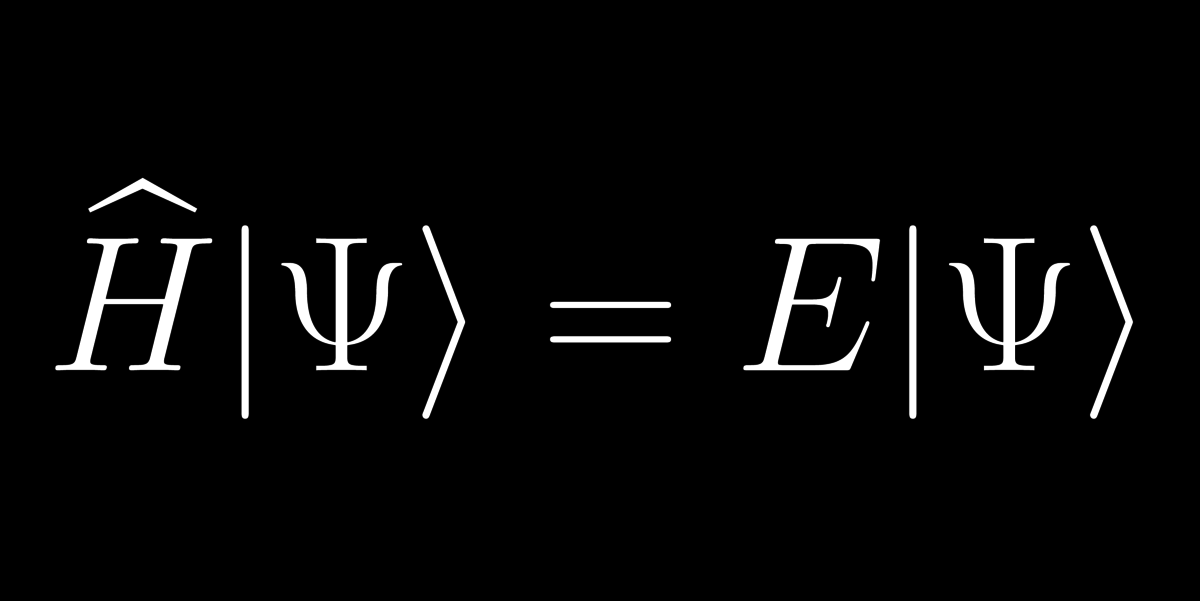
Mely elemek alkotják a Napot? Főleg hidrogén(≈75%) és hélium(≈24%). De honnan tudjuk? Onnan, hogy megoldottuk az időfüggetlen Schrödinger-egyenletet, így megkaptuk az egyes atomok E energiaszintjeit, majd ezeket beazonosítottuk a Nap fényében (elnyelési színkép).
32: Kvaterniók

A számítógépes játékok grafikájától kezdve, a vezeték nélküli adattovábbításon keresztül, egészen a modern fizikáig terjednek a kvaterniók alkalmazásai. Ezek az a+bi+cj+dk alakú számok (a,b,c,d∈ℝ) a valós ℝ és a komplex ℂ számhalmazok bővítését adják.
31: Legkisebb hatás elve

"A Természet a minimumra törekszik". Ezt ragadja meg a legkisebb hatás elve, ami elméleti háttérként szolgál az általános tömegvonzás törvényének, a Maxwell-egyenleteknek, a Schrödinger-egyenletnek, és az általános relativitáselméletnek.
30: A kontinuum számossága

Mennyi egész szám van? ∞ Na és törtszám? ∞ És a valós számok? ∞ Ezek közül melyik végtelen a legnagyobb? Van-e egyáltalán értelme ennek a kérdésnek? De van ám! Megmutatható, hogy egész- és törtszámból ugyanannyi van, de valós számból több!
29: Maxwell-egyenletek

Internet, TV, telefon, autók, MRI..ezek egyike sem létezne a Maxwell-egyenletek nélkül. Az elektromos és mágneses jelenségeket egyesítő összefüggések jelentették a 19. századi fizika csúcsát és a 20. századi technológiai fejlődés alapját.
28: Poisson-eloszlás
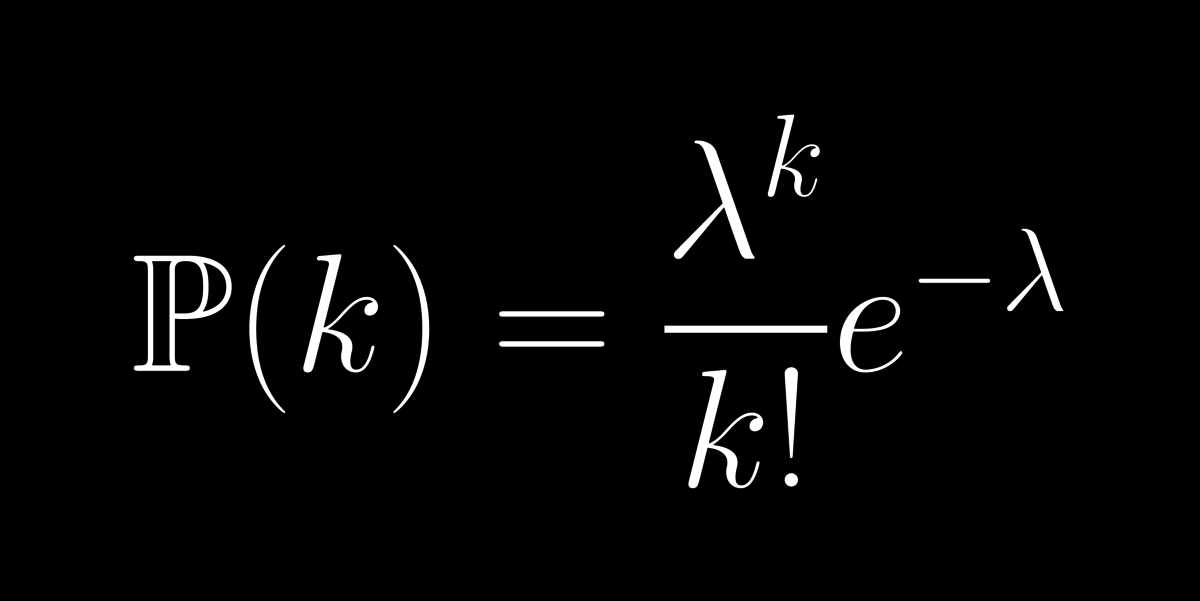
Hány email-t fogsz ma kapni? Hány mutáció lesz a DNS-ed egy szakaszán? Óránként mennyi hullócsillagot látsz este a derült égbolton? Évente hány porosz katonát ért halálos lórúgás 1875-94 között? Ez mind-mind Poisson-eloszlást követ!
27: Navier–Stokes-egyenletek

1 millió dollár jár annak, aki megoldja ezt az egyenletet! A folyadékok áramlását leíró Navier–Stokes-egyenletek hasznosságban és nehézségben egyaránt páratlanok. Modellezhető velük az időjárás, de pl. áramvonalasabb autók tervezésére is jók.
26: Bell-egyenlőtlenség

"Isten nem kockajátékos", így fejezte ki Einstein, hogy szerinte a véletlennek nincs helye az atomok világában. Az csupán tudásunk részlegessége (rejtett paraméterek) miatt tűnik annak. Ezt cáfolta meg a Bell-egyenlőtlenség és az arra épülő kísérletek!
25: Hővezetés egyenlete

Hogyan keveredik el egy festékcsepp a vízben? Miként melegedik fel egy sütőlap? Az ilyen kiegyenlítődési folyamatokat írja le ez az egyenlet, amelyet épp a fenti példák miatt szokás diffúziós vagy hővezetési egyenletnek hívni.
24: Csebisev-egyenlőtlenség
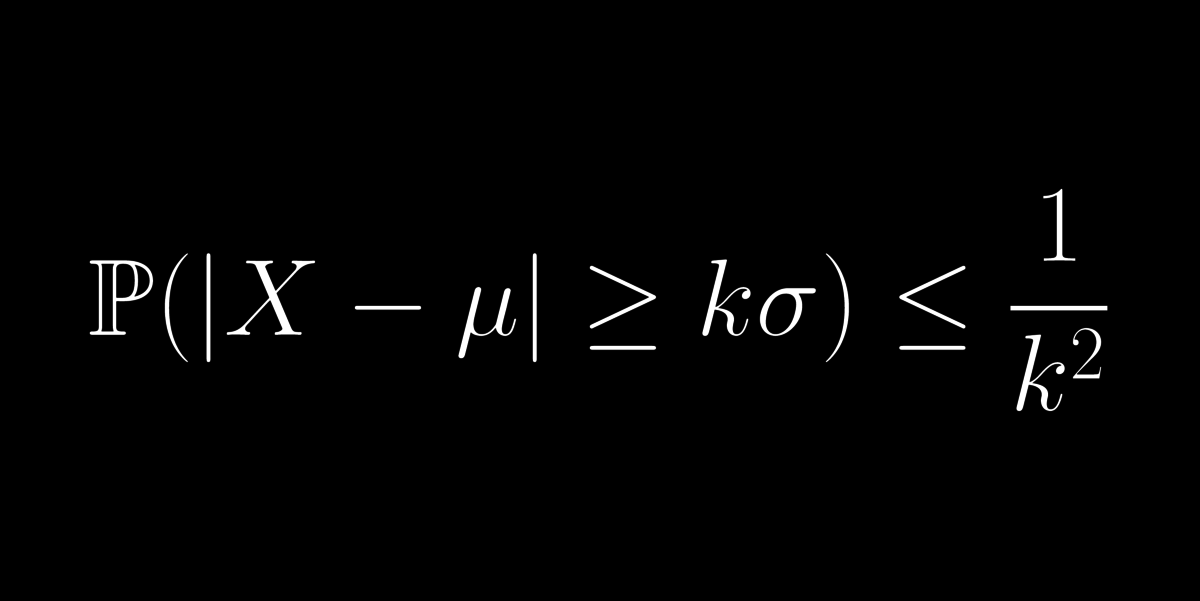
Mennyire valószínű, hogy egy mérési eredmény az átlagos értéktől egy adott számnál jobban eltérjen? A Csebisev-egyenlőtlenség szerint annak a valószínűsége, hogy az átlagtól való eltérés a szórás $k$-szorosánál nagyobb legfeljebb $1/k^2$.
23: Inverz négyzetes törvény

Ilyen ártatlannak tűnő 1/r² alakú törvény bukkan fel a Nap körül keringő bolygók, a fáról lepottyanó alma, és a Hidrogén-atom elektronjának leírásakor. Nem is csoda, hogy Newton gravitációs elmélete a tudomány egyik legnagyobb sikertörténete.
22: Black–Scholes-egyenlet

A Black–Scholes-egyenlet egy tőzsdemodell az európiai típusú opciók beárazására. Az egyenlet tanulsága, hogy létezik egy pontos ár és lehet úgy kereskedni, amivel a kockázat kiküszöbölhető. Az eredményt 1997-ben közgazdasági Nobel-díjjal jutalmazták.
21: Geodetikus egyenlet

Gyakran halljuk, hogy két pont között a legrövidebb út az egyenes. De mi van akkor, ha hepehupás a talaj? És ha a Föld két városa közötti legrövidebb utat keressük? Vagy ha a görbült téridőben utazunk? Ezekre ad választ a geodetikus egyenlet.
20: Prímszámtétel
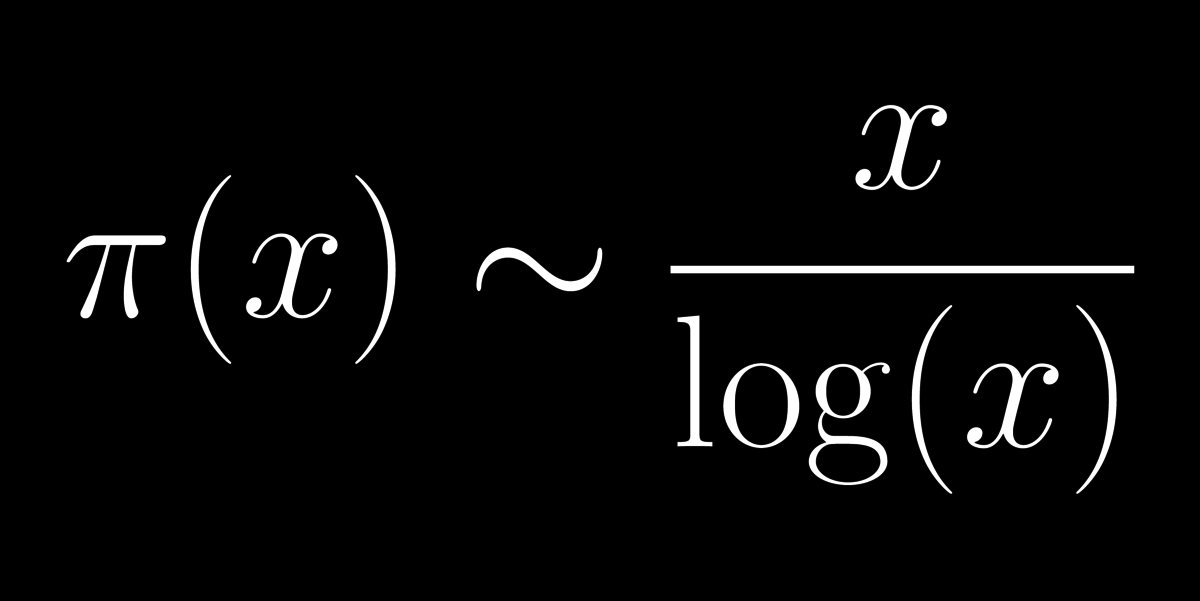
Habár a prímszámok felbukkanása az 1,2,3,... sorozatban véletlenszerűnek tűnhet, mégis található bennük rendszer. Ilyen például a prímszámtétel, amely az x-nél kisebb prímek π(x) számára ad egy becslést, ami x növelésével egyre pontosabb.
19: Dirac-egyenlet
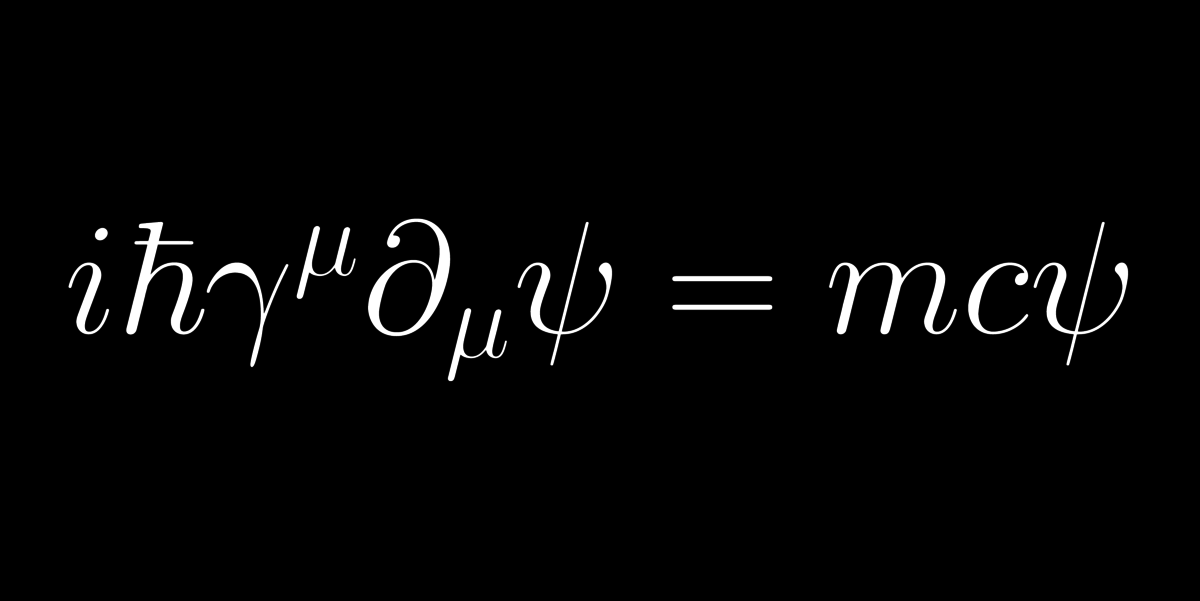
Ezzel az egyenlettel Dirac 1928-ban megjósolta(!) az antianyag létezését, amit pár évvel később kísérletileg is igazoltak. A Dirac-egyenlet az elektront írja le, de van olyan megoldása is, amely egy "pozitív töltésű elektron"; ez a pozitron.
18: Lotka–Volterra-egyenletek

A Lotka–Volterra-egyenletek a ragadozó-zsákmány párharcot modellezik. Az első a zsákmány számának változását írja le, a második a ragadozókét. Ha sok a zsákmány (x nagy), akkor ragadozókból is több lesz (y nő) már, ha "összefutnak" (β,δ≠0).
17: Általános gáztörvény
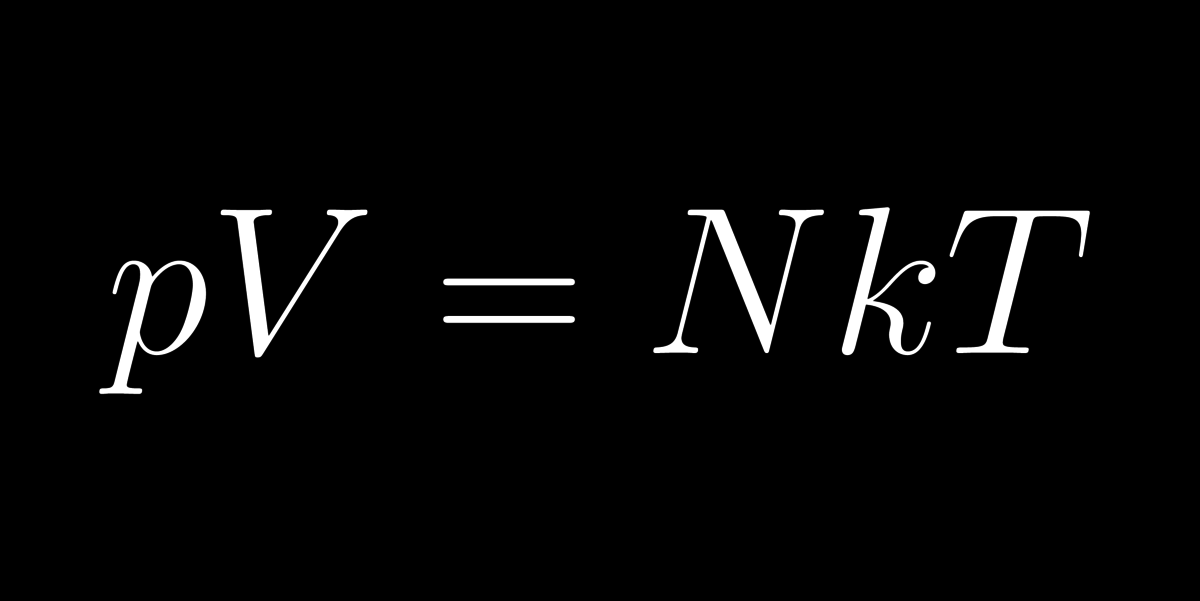
Egy gázt felfoghatatlanul sok atom alkot, amelyek mindenfelé repdesve nagy zűrzavar benyomását keltik. Az általunk érzékelt világban az összevisszaságból mégis rend születik. Az általános gáztörvény ennek elegáns leírása.
16: Korteweg–de Vries-egyenlet
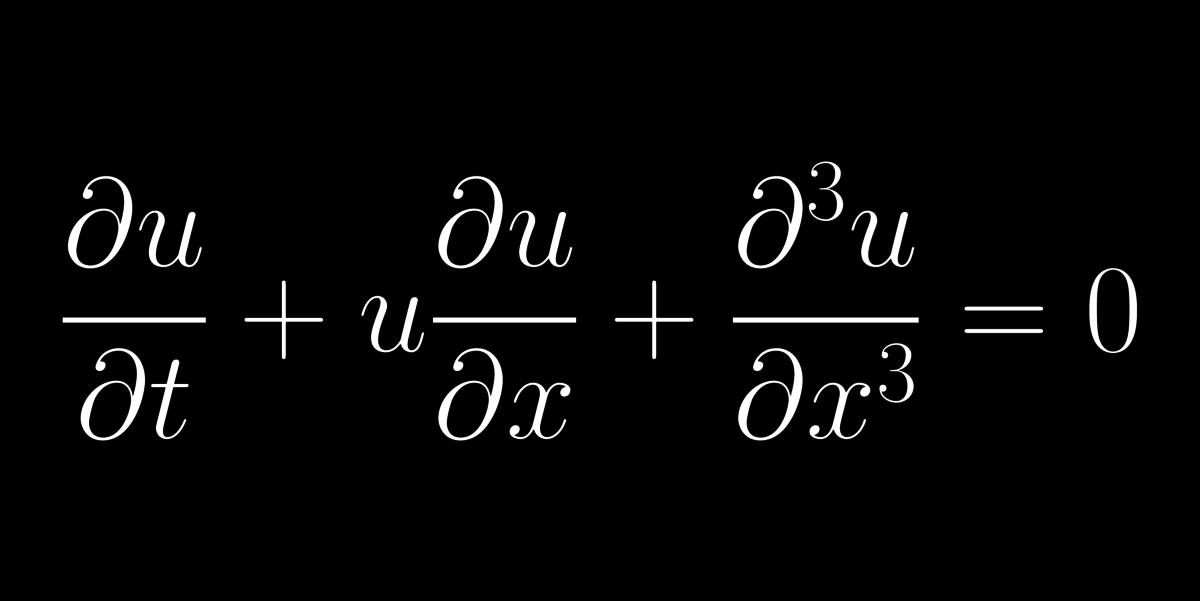
A Korteweg–de Vries-egyenlet írja le a sekély vízfelszínen keletkező és a plazma állapotú anyagokban megfigyelt hullámokat. A leghíresebb hullámokat modellező egyenlet, aminek vannak stabil, részecskeszerű megoldásai. Ezek az ún. szolitonok.
15: Einstein-egyenletek

Az Einstein-egyenletek a gravitációt a téridő geometriájával írják le. Eszerint az anyag meggörbíti a teret (és időt), ami cserébe 'megmondja' az anyagnak, hogy miként mozogjon. Ez talán a legnagyobb paradigmaváltás, amit a fizika valaha látott.
14: Pitagorasz-tétel

A Pitagorasz-tétel a világ talán legismertebb képlete. A derékszögű háromszögek oldalhosszait kapcsolja össze: a,b befogók (rövidebb oldalak), c átfogó (leghosszabb oldal). Legalább 4000 éve ismeri az emberiség és rengeteg bizonyítása, általánosítása létezik.
13: Ising-modell

Ez a képlet írja le, hogy hogyan jönnek létre a mágnesek! Ez az Ising-modell, amiből az is kiszámolható(!), hogy egy bizonyos hőmérséklet felett még a vas és a kobalt is elvesztik mágneses tulajdonságuk.
12: Stirling-formula
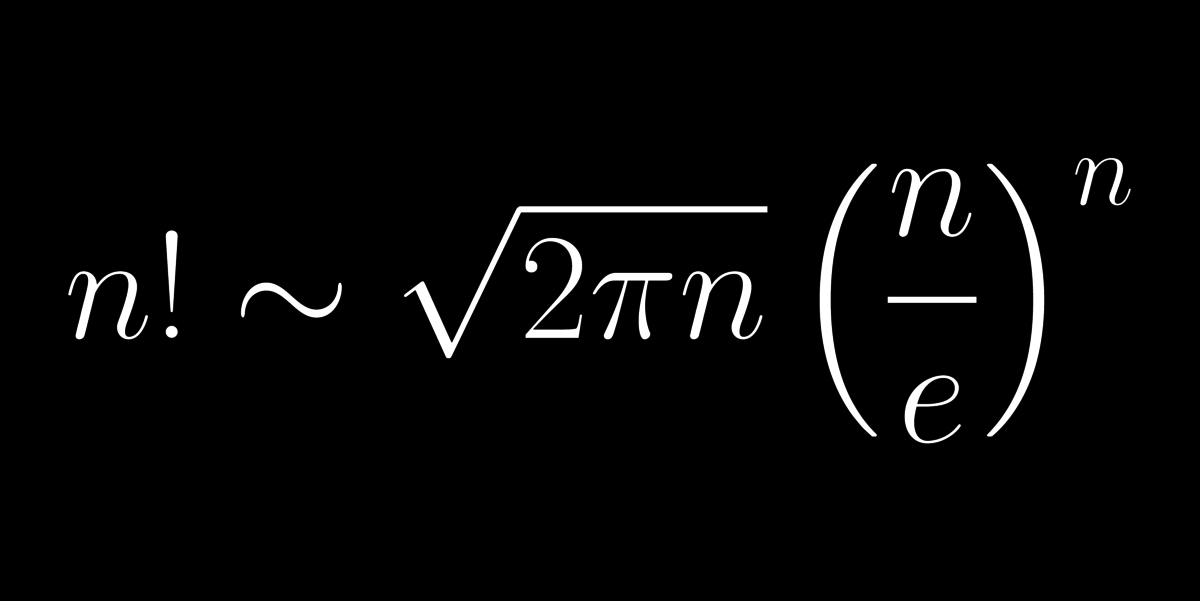
3 különböző dolgot 6-féle sorrendbe tehetünk: ABC, ACB, BAC, BCA, CAB, CBA. A sorrendek számát a faktoriális adja meg: 3!=3×2×1=6. A Stirling-formula erre ad egy szép közelítő képletet, ami annál pontosabb minél több dologról van szó.
11: Bekenstein-Hawking formula

A Bekenstein-Hawking képlet kifejezi egy fekete lyukhoz rendelt entrópiát (S) az eseményhorizont méretével (A). A formula csodálatosan köt össze termodinamikai (k), gravitációs (G) és kvantumos (ħ) mennyiségeket.
10: Normális eloszlás

Az emberek magasság, súly, cipőméret, vérnyomás, stb. szerinti eloszlása mind ezzel képlettel írható le ($\mu$ az átlag, $\sigma$ a szórás). Ez a normális eloszlás, amely szinte mindig előbukkan, ha valamilyen véletlen mérőszámról készítünk statisztikát.
09: Entrópia
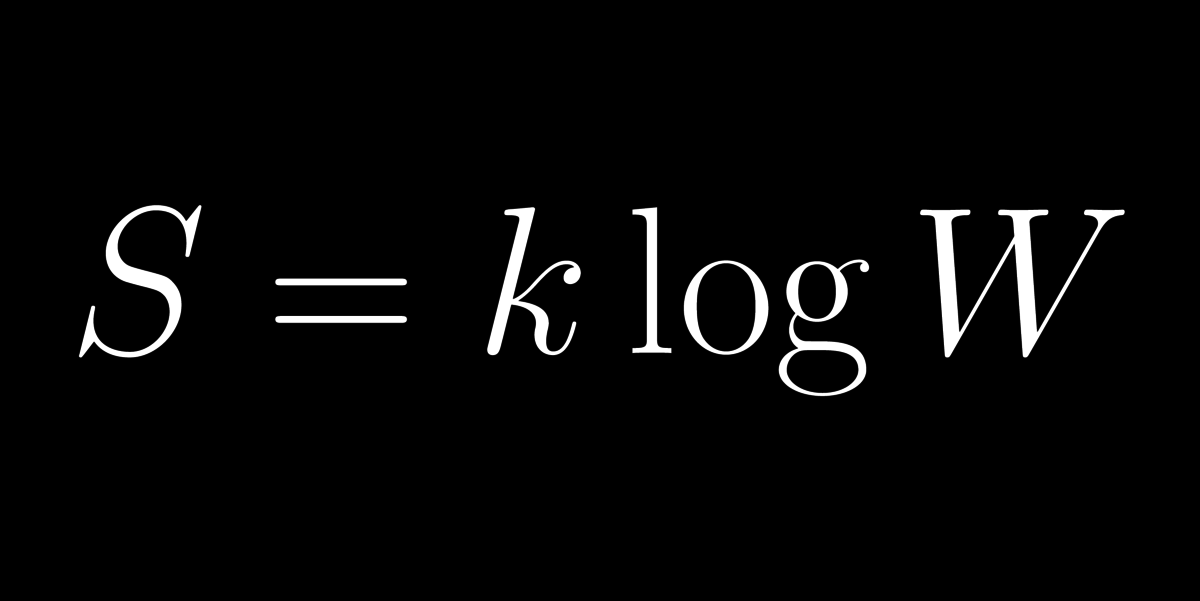
Az entrópia (S) a rendezetlenséget méri. A világegyetem teljes entrópiája az idő múlásával nem csökkenhet, ezért tudjuk megkülönböztetni a múltat a jövőtől (az időnek van iránya). A képletet Boltzmann fedezte fel (a sírkövébe is belevésték).
08: Logisztikus leképezés

Ebben az egyszerű képletben megbújik a káosz. A logisztikus leképezés egy populációdinamikai modell, amely egy $x_0$ ($ 0 < x_0 < 1 $) értékből indulva évről-évre megadja a népesség 'telítettségét'. $ r > 3,57 $ esetén egy kicsi zavar $x_0$-ban idővel felerősödik.
07: Schrödinger-egyenlet

Ami Newtonnak $F=ma$, az Schrödingernek a fenti egyenlet. Ez az atomok 'kvantumos' világának mozgásegyenlete. Fontos tulajdonsága, hogy lineáris, azaz megoldások keveréke is lehet megoldás. Ezért lehet Schrödinger macskája félig $|\Psi_{\mathrm{élő}}\rangle$, félig $|\Psi_{\mathrm{holt}}\rangle$.
06: Laplace-egyenlet

Milyen melegek lesznek a lakás egyes részei, ha a falakat fix, de falanként más-más hőmérsékleteken tartjuk? A Laplace-egyenlet megoldása ilyen 'egyensúlyi' kérdésekre ad választ. Sőt még a Coulomb-törvény is kihozható belőle!
05: Fourier-transzformáció
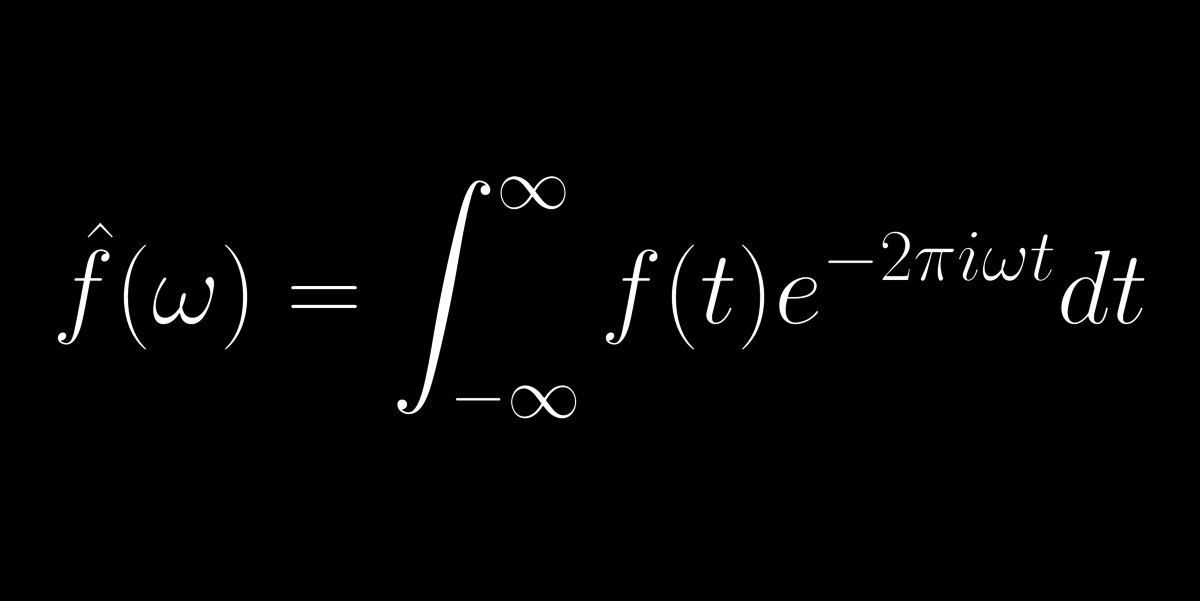
Aki tud hallás után kottázni, ezt a képletet alkalmazza a fejében/fülében!! A Fourier-transzformáció egy (bonyolult) $f(t)$ bemeneti jelet, pl. a hangot, összetevőire bontja és megadja az $\hat{f}(\omega)$ frekvencia-eloszlást.
04: Hosszúságrövidülés

A hosszúságrövidülés az egyik legmeglepőbb következménye Einstein speciális relativitáselméletének. Eszerint az 1 km hosszú (L₀) kocsisort 1 m hosszúnak (L) méri/látja az, aki a fénysebesség (c) 99,99995%-ával suhan el mellette.
03: Euler képlete poliéderekre
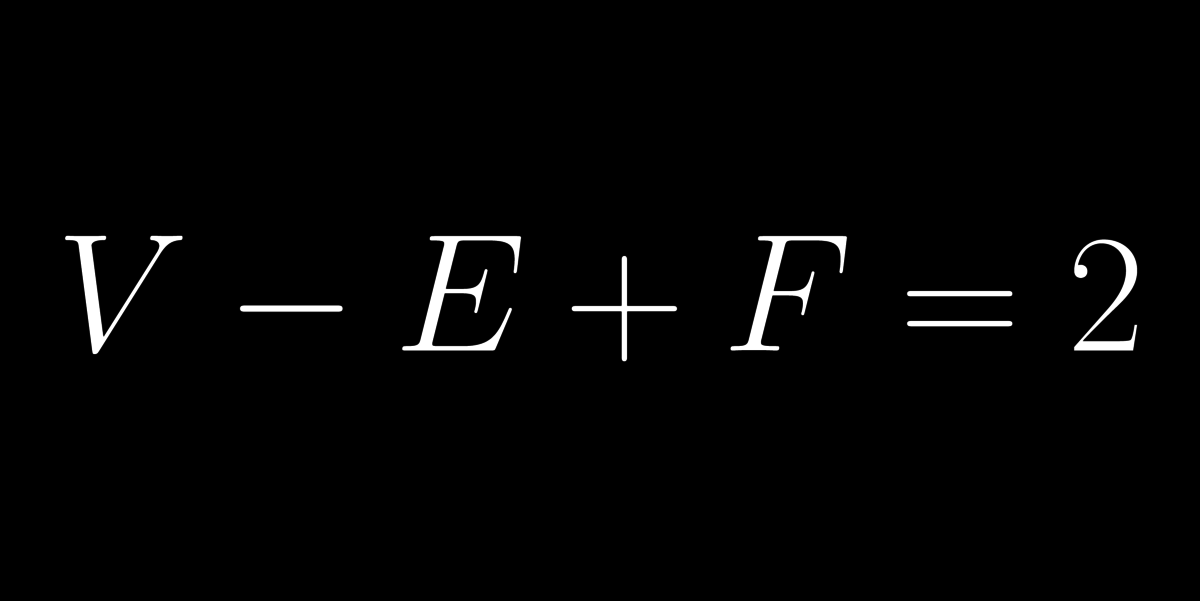
Minden sokszöglapokból felépülő (konvex) testre (pl. kockára vagy 'piramisra') igaz Euler képlete. Eszerint a csúcsok száma (V) mínusz az élek száma (E) plusz a lapok száma (F) egyenlő kettővel. Kockára: V=8, E=12, F=6. Keressetek más példákat!
02: Newton II. törvénye

Newton II. törvénye egy bámulatos felfedezés és a fizika egyik alapegyenlete. Eszerint egy testre ható erők összessége (F) egyenlő a test tömegének (m) és gyorsulásának (a) szorzatával. Érvényes (szinte) mindenre, ami mozog!
01: Euler-azonosság
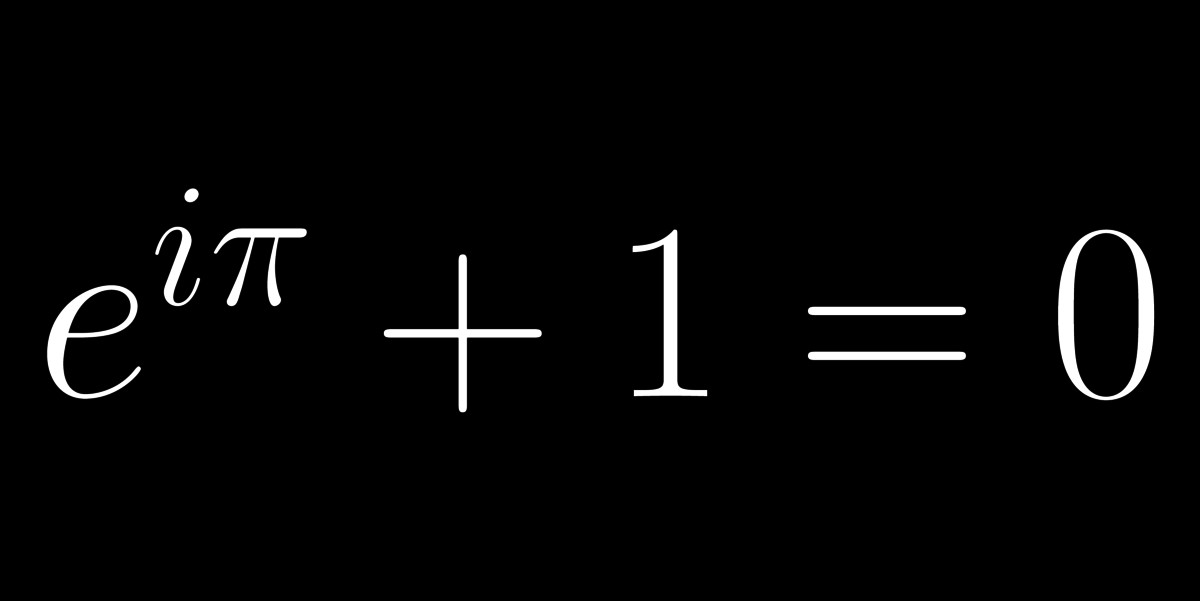
Az Euler-azonosság a matematika egyik csodája, amely az öt legfontosabb számot köti össze: 0, 1, π = (kör kerülete/átmérője) ≈3.14159, e = (ennyi lesz 1 Ft-ból 1 év múlva 100% kamat *folyamatos* jóváírásával) ≈2.71828, i = (-1 négyzetgyöke!)