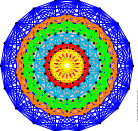
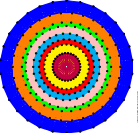
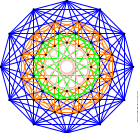
Exce6ptionally Be7autiful Symme8tries
by Tamás F4erenc G2örbe
The string arts are installed in the Bolyai Institute at the University of Szeged.
| History |

The classification of (semi)simple Lie algebras over the field of complex numbers is regarded by many as a jewel of mathematics. It was first described by German mathematician Wilhelm Killing in a series of papers published between 1888-1890. A more rigorous proof (and the case of real Lie algebras) was presented by Élie Cartan in his 1894 PhD thesis. In 1947 the 22-year old Eugene Dynkin worked out a modern, streamlined proof of the classification theorem. The theorem states that every semisimple complex Lie algebra is a "sum of building blocks", most of which belong to one of four infinite families. These are denoted by A$_n$, B$_n$, C$_n$, D$_n$, where $n$ is an arbitrary positive integer. Surprisingly, there exist five exceptional "building blocks" that don't fit into the above families. They are named E$_6$, E$_7$, E$_8$, F$_4$, G$_2$. 

The classification theorem heavily relies on abstract mathematical objects called root systems, which are symmetric configurations of vectors (usually) sitting in higher dimensional space. The dimension of this space is indicated by the subscripts, e.g. E$_8$ lives in an $8$-dimensional Euclidean space. |
| How it's made |
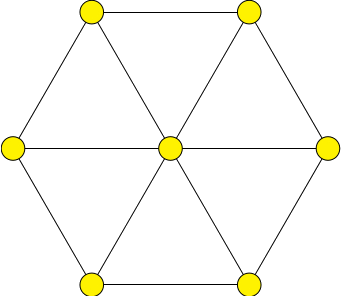
The frame of a cube can cast shadows of different shapes, but only a few orientations lead to the most symmetric shadows, namely the projections through one of the four body diagonals. See the image on the right. The method of finding the "most symmetric shadows" can be generalized to higher dimensions, and this is how the string arts of the exceptional root systems E$_6$, E$_7$, E$_8$, F$_4$, G$_2$ were made. The needles of the string arts point where the end points of root vectors land after projection. 
The connections are obtained by connecting every vector with their nearest neighbours before the projection.$^\dagger$ A fun fact is that due to the left-right symmetry of the connections we have an even number of threads meeting at every needle, In graph theory such a structure is called an Eulerian Circuit. meaning that the connections with different colours can be drawn using a single, but really long piece of thread without cutting.$^\ddagger$ $^\dagger$ There are some extra connections in the case of G$_2$. |
Gallery
Media appearances
- Exceptionally Beautiful Symmetries (Newsletter of the LMS, May 2021) [link]
- Enchanting Symmetries, the Gems of Mathematics (A public lecture in Hungarian, November 2017) [link]
- Maths is Beautiful (An interview in Hungarian, November 2016) [link]
- Enchanting Symmetries - spectacular mathematics (An interview in Hungarian, June 2016) [link]
- Temporary exhibit in the Hungarian Academy of Sciences Building (Szeged) between Feb 23-Mar 31, 2016 [link]
- Coxeter Projection of Exceptional Root Systems (A blogpost in English, October 2015) [link]
- E8: An Exceptionally Beautiful Piece of Mathematics (A blogpost in English, May 2015) [link]
Poster
Click the image to download a poster. [PDF, 3.7 MB]