Welcome to my website!

A komplex számtest feletti féligegyszerű Lie-algebrák osztályozása sokak szerint a matematika egyik páratlan eleganciájú és fontosságú gyöngyszeme, melyet elsőként Wilhelm Killing írt le 1888-1890 között megjelenő dolgozataiban. Ezt tette precízzé Élie Cartan 1894-es Ph.D. disszertációjában, aki a valós esetet is kidolgozta. 1947-ben az akkor 22 éves Eugene Dynkin munkája nyomán modern, letisztult formát nyert az osztályozás. Eszerint bármely komplex féligegyszerű Lie-algebra felbontható olyan egyszerű "építőkockák összegére", amelyek négy, végtelen sok elemet tartalmazó családba rendezhetőek.

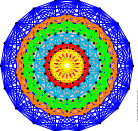
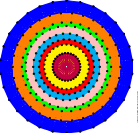
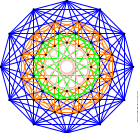
Ezek jele A$_n$, B$_n$, C$_n$, D$_n$, ahol $n$ tetszőleges pozitív egész szám, azonban létezik öt kivételes, egyik fenti családba sem tartozó Lie-algebra, jelben E$_6$, E$_7$, E$_8$, F$_4$, G$_2$. Az osztályozás matematikai bizonyításban kulcsszerepet kapnak a minden információt magukban hordozó gyökrendszerek, amelyek a számok által jelzett dimenziós térben vektorok nagy szimmetriával bíró konfigurációi.

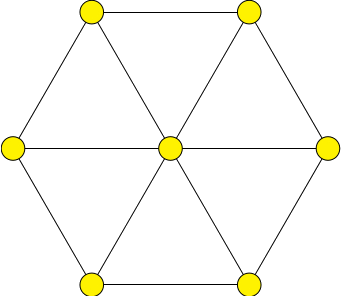
Egy kocka sokféle árnyékot vethet, de a maximális szimmetriával rendelkező vetületet csupán néhány kitüntettet irányból, nevezetesen a négy testátló bármelyikével párhuzamosan világítva kaphatjuk meg. Lásd a mellékelt ábrát. Ez az eljárás magasabb dimenziókra is általánosítható, így az E$_6$, E$_7$, E$_8$, F$_4$, G$_2$ kivételes gyökrendszerek "legszimmetrikusabb árnyéka" is elkészíthető. A bemutatott fonalgrafikák gombostűi által jelölt pontok is így keletkeztek.

Még a vetítés előtt minden gyökvektort összekötöttünk legközelebbi társaival, így jöttek létre a pontokat összekötő élek$^\dagger$. További érdekesség, hogy a bal-jobb szimmetria miatt minden pontnál páros sok egyazon színű él fut össze, ezért ha a megfelelő körre illeszkedő pontok közül bármely kettő elérhető egymásból az adott szín mentén$^\ddagger$, akkor egyetlen (nagyon hosszú) cérnaszálból ismétlés nélkül húzható be minden él. A gráfelméletben ezt nevezik Euler-körnek.

$^\dagger$ G$_2$ esetén további élek is behúzásra kerültek. $^\ddagger$ Ez egy esetben nem teljesül. Vajon hol?